[표본 통계량의 분포] t분포
표본 통계량이란?
앞의 글에서 잠깐 이야기 했듯이 모집단 전체를 분석할 수 없기 때문에 표본을 추출하게 됩니다.
그 표본에서 구한값을 표본 통계량이라고 합니다.(ex. 표본평균, 표본분산,표본 비율)
이러한 값들을 표본을 추출할때마다 값이 변하기 때문에 확률변수 라고합니다.
위의 확률변수들이 가지는 분포를 확률 분포라고 합니다.
표본평균의 분포
우선 표본 평균의 식은 다음과 같습니다.
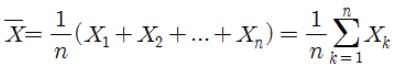
표본평균은의 분포는 중심극한정리에의해 표본의 수(n)가 많아 질수 록 정규분포에 근사합니다.(n>=30)
정규분포를 식으로 나타낸다면 아래와 같습니다.
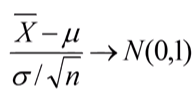
이때 모집단의 표준편차 시그마를 모르는 경우가 발생합니다. 이때 표본의 표준편차를 사용하게 됩니다.
이때의 식은 아래와 같습니다.
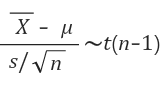
위의 식은 정규분포가 아닌 t분포를 따릅니다.
표본의 값 x1~xn이 평균이 뮤이고 분산이 시그마 제곱인 정규분포에서 뽑은 확률표본일때 x bar를 표준화 할때
시그마가 아닌 s를 사용하면 t 분포를 따르게 됩니다.
* 확률표본 : 표본들이 동일한 집단에서 독립적으로 뽑은 값
s를 추정할 때 사용한 샘플의 개수에 따라서 분포의 모양이 다르기 때문에 t분포 식안에 샘플의 개수를 적어주는데
이는 n이 아닌 n-1로 작성하는 이유는 자유도를 사용하기 때문입니다.
t분포의 그래프
정규분포의 그래프와 자유도에 따른 t분포는아래 그림과 같습니다.
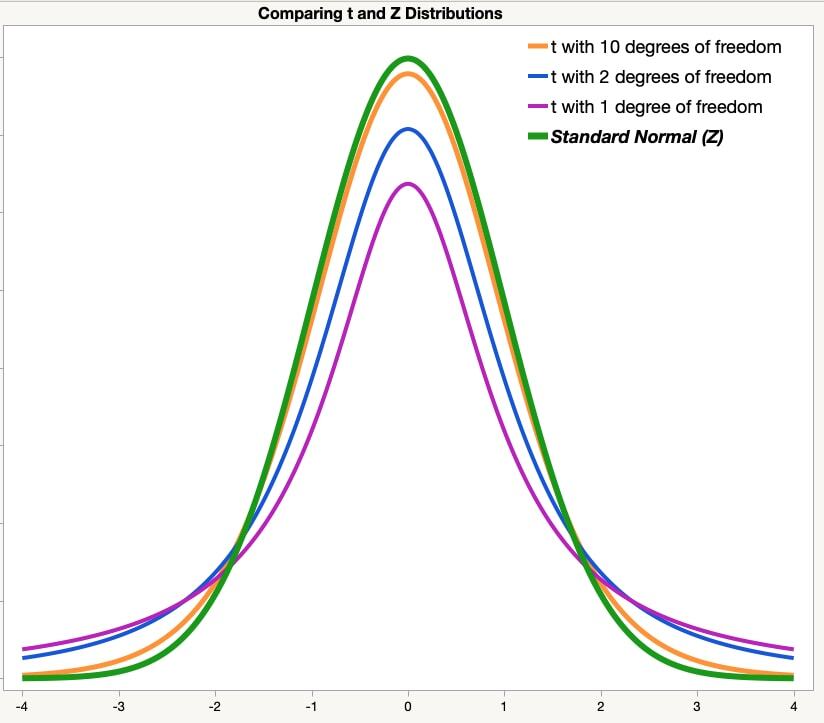
표준정규분포의 그래프는 좌우가 대칭인 종모양의 그래프입니다.
t분포의 그래프는 정규분포와 비슷한 모양을 나타냅니다.
t분포의 그래프 모양은 표본의크기와 관계가 있습니다. 표본의 크기가 많아지면 모수와 가까워 지기때문에
S의 값이 시그마의 값과 유사하게 됩니다.
t분포의 자유도는 표본의 크기에 1을 뺀값이기 때문에 표본의 크기가 커질수 록 자유도가 커지게 됩니다.
그렇기 때문에 위의 그림과 같이 표본의크기가 커질수록 t분포는 정규분포의 그래프 모양과 같아지게 됩니다.
자유도란?
자유로운 표본의 개수로 생각하면 알기 쉽습니다.
이론적 정의= 추정값을 구하는데 사용된 정보의 개수입니다.
자유도가 n-1개인 이유는

위의 식에서 이미 x bar를 알고 있기 때문에 표본하나를 잃습니다.
이를 쉽게 이해하기 위해서 예를 들자면
학생 A의 4과목 평균이 90점이고 국,영,수 점수가 각각 90,91,92일때 사회과목의 점수는 87이라고 추측할 수 있습니다.
이는 평균이 주어졌기때문에 4개중에 3개만 알고 있어도 정보를 알 수 있기때문입니다.
따라서 자유로운 표본의 개수(=자유도)는 3(4-1)이 됩니다.
표본의 개수보다 자유도라는 개념을 사용하는 이유는 수학적 이론에 적합하기 때문입니다.
t값 구하기
자유도와 유의확률을 통해 t분포표를 참고해 t값을 구할 수 있습니다.
t값을 구하는 방법은 Python에서 scipy.stats모듈에서 지원 하고있습니다.
t 값을 Python으로 구하는 방법을 알아보도록 하겠습니다.

위와 같이 총행의 길이가 55개인 DataFrame을 df에 저장했습니다.
이때 신뢰구간을 95%로 하고 상위 5%의 t값을 구해보도록 하겠습니다.
from scipy.stats import t
# 자유도 구하기
dof = len(df)-1
# t값 소수3째 자리까지 나타내기
round(t.ppf(0.95,dof),3)위의 코드를 실행하게 되면 자유도는 54, t값은 1.674가 나타나게 됩니다.
하위의 값을 구하기 위해서는 위의 코드에서 도출된 t값에 -부호를 붙여주면 됩니다.

위 그림은 t 분포에서 찾은 상위 5%의 t값을 그래프로 나타낸 것입니다.