[Python] T-검정의 종류와 구현3(대응하는 비모수 검정)
이전 글에서 독립 표본 t 검정에 대해 알아봤습니다.
이번 글에서는 대응 표본 t 검정에 대해 알아보겠습니다.
1. 대응표본 T-검정(Paired smaple t-test)
대응 표본 T-검정이란 동일한 집단의 두 관측 값을 비교하여 집단 간의 평균 차이를 평가하는 통계적 방법입니다.
예를 들어, 다이어트 약을 테스트하기 위해 추출한 집단 A에 대해 약을 먹기 전 몸무게와 약을 먹은 후의 몸무게를
측정하여 동일한 집단 간의 관측 값을 비교하여 차이를 검정하는 방법입니다.
가설
대응 표본 T-검정의 가설은 아래와 같습니다.
귀무가설(H0) : "두 집단 간의 차이가 없다."
대립가설(H1) : "두 집단 간의 차이가 있다."
전제조건
대응 표본 T-검정을 사용하기 위해서는 다음과 같은 조건을 충족해야 합니다.
- 전후 관측값을 측정하는 집단이 동일해야한다.
- 예를 들어 다이어트 약에 관해서 실험을 하는데 동일한 다이어트 약을 복용하기 전의 환자와 복용한 후의 환자는 동일해야 합니다.
- 측정 대상의 정규성
- 정규성을 만족하지 못한다면 비모수 검정을 실시해야 합니다.
- 측정값의 쌍의 독립성
- 측정을 하기 전의 그룹이 측정을 한 후의 그룹에 대해 영향을 주지 않아야 합니다.
- 등분산성
- 이상치 제거
- 이상 값에 민감하기 때문에 대응 표본 T-검정을 실행하기 전에 이상치를 제거해 줍니다.
Python 대응표본 T-검정
Pyhton에서 대응 표본 T-검정을 사용하기 위해서는 scipy 라이브러리 stats 모듈의 ttest_rel 함수를 사용할 수 있습니다.
ttest_rel 함수의 매개변수는 아래와 같습니다.
scipy.stats.ttest_rel(a, b, axis=0, nan_policy='propagate', alternative='two-sided', *, keepdims=False)
- a,b : 비교할 두 개의 배열(before, after)입니다. 두 배열을 동일한 형태(shape)를 가져야 합니다.
- nan_policy({'propagate', 'omit', 'raise'}) : NaN 값을 처리하는 방법입니다.
- propagate : NaN 값이 포함되어 있으면 NaN 값이 출력됩니다.
- omit : 계산을 수행할 때 NaN 값이 생략됩니다.
- raise : NaN 값이 있다면 valueError가 발생합니다.
- alternative :대립가설을 정의합니다. 기본 설정은 'two-sided'입니다.
- 'two-sided': 비교하는 두 샘플의 분포 평균이 서로 다릅니다.
- 'less': 첫 번째 샘플의 분포 평균이 두 번째 샘플의 분포 평균보다 작습니다.
- 'greater': 첫 번째 샘플의 분포 평균이 두 번째 샘플의 분포 평균보다 큽니다.
구현
데이터를 불러옵니다.
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/rel2.csv')
우선 이상치가 있는지 boxplot을 통해 확인합니다.
import seaborn as sns
sns.boxplot(y = 'after',data = df)
before 열에 이상치가 있는 것을 확인할 수 있습니다.
이상치를 평균으로 대체한 후 다음 조건을 부합하는지 확인합니다.
def detect_outliers(data):
# 이상치를 정의할 상위 및 하위 Whisker 범위를 계산합니다.
q1 = data.quantile(0.25)
q3 = data.quantile(0.75)
iqr = q3 - q1
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr
# 이상치를 감지합니다.
outliers = (data < lower_bound) | (data > upper_bound)
return outliers
# 이상치를 평균으로 대체
def replace_outliers_with_mean(data):
outliers = detect_outliers(data)
mean_value = data[~outliers].mean() # 이상치가 아닌 데이터들의 평균을 mean_value값에 저장합니다.
data[outliers] = mean_value # 이상치에 해당하는 값들을 평균을로 대체합니다.
return data
df['before'] = replace_outliers_with_mean(df['before'])
sns.boxplot(data = df[['before','after']])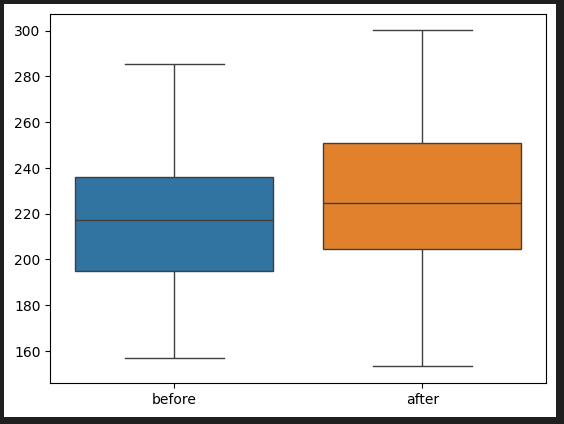
이상치가 정상적으로 제거된 것을 확인할 수 있습니다.
before, after 열의 데이터들이 정규성, 등분산성, 독립성을 만족하는지 확인합니다.
from scipy.stats import shapiro, levene, chi2_contingency
# 각각의 데이터가 정규성을 만족하는지 확인
print(shapiro(df['before']))
print(shapiro(df['after']))
# 등분산성을 만족하는지 확인
print(levene(df['before'],df['after']))
# 독립성을 만족하는지 확인
crosstab = pd.crosstab(df['before'],df['after'])
chi2_stat, p_value, dof, expected = chi2_contingency(crosstab)
print('p_value=',p_value)
정규성, 등분산성, 독립성의 검정 결과의 pvalue가 0.01 이상이기 때문에 모든 조건을 만족한다고 볼 수 있습니다.
그러므로 대응 표본 T-검정을 실행합니다.
from scipy.stats import ttest_rel
ttest_rel(df['before'],df['after'])
결과 해석
pvalue의 값이 0.008로 0.01보다 작은 값을 나타내기 때문에 유의수준 1% 하에서도 두집단의 값에는 차이가 있다고 할 수 있습니다.
따라서 대립가설("실험 전후의 값에는 차이가 있다.")을 채택합니다.
대응하는 비모수 검정
1. Wilcoxon 부호-서열검정 (Wilcoxon sugned-rank test)
Wilcoxon 부호-서열검정은 기본 가정사항이 없기 때문에 모수 검정에 비해 쉽게 사용할 수 있습니다.
Wilcoxon 부호-서열검정의 가설 역시 대응표본 t-검정과 같습니다.
가설
귀무가설(H0) : "두집단간의 차이가 없다."
대립가설(H1) : "두집단간의 차이가 있다."
Python Wilcoxon 부호-서열검정
Wilcoxon 부호-서열검정은 파이썬의 scipy 라이브러리 stats 모듈의 wilcoxcon 함수를 사용할 수 있습니다.
우선 데이터를 가져옵니다.
import pandas as pd
import seaborn as sns
df = pd.read_csv('https://raw.githubusercontent.com/Datamanim/datarepo/main/scipy/rel1.csv')
sns.boxplot(data = df[['before','after']])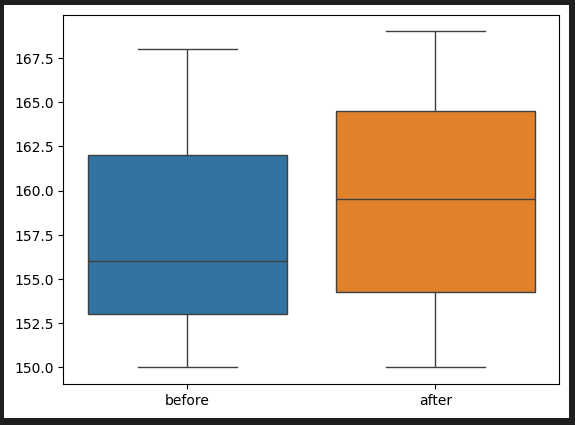
이상치는 존재하지 않는것으로 확인되기 때문에 정규성,등분산성,독립성 검정을 실시하도록 하겠습니다.
from scipy.stats import shapiro, levene, chi2_contingency
# 정규성 검정
print(shapiro(df['before']))
print(shapiro(df['after']))
# 등분산 검정
print(levene(df['before'],df['after']))
# 독립성 검정
crosstab = pd.crosstab(df['before'],df['after'])
chi2_stat, p_value, dof, expected = chi2_contingency(crosstab)
print('p_value=',p_value)
after열은 정규성을 만족하지 못하기 때문에 비모수 검정을 실기해야 합니다.
등분산성, 독립성 역시 p_value값이 0.05보다 크기 때문에 만족하지 못합니다.
그렇기 때문에 대응표본 T-검정에 대응하는 비모수적 검정인 Wilcoxon 부호-서열검을 사용합니다.
from scipy.stats import wilcoxon
print(wilcoxon(df['before'],df['after']))
결과해석
pvalue값이 0.12로 0.05보다 큰값을 가지기 때문에 귀무가설("두집단의 전후는 차이가 없다.")를 채택합니다.