1. 단순선형회귀분석
하나의 독립변수가 종속변수에 미치는 영향을 추정할 수 있는 통계기법

y : 종속변수 값
x : 독립변수 값
B0 : 선형 회귀식의 절편
B1 : 선형 회귀식의 기울기
ε : 오차항, 독립적이며 N의 분포를 이룬다.
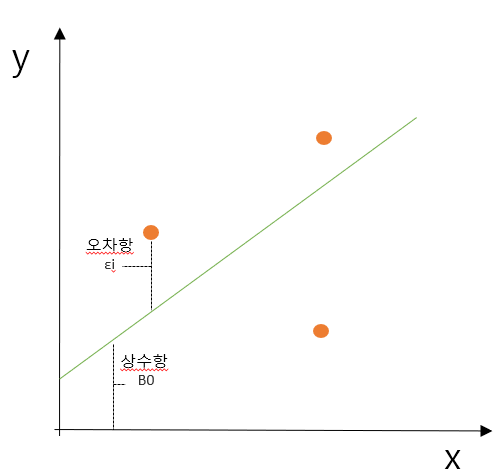
회귀분석에서 검토사항
1. 회귀계수들이 유의미한가?
- 해당 계수의 t 통계량의 p-값이 0.05보다 작으면 해당 회귀계수가 통계적으로 유의 하다고 볼 수 있다.
2. 모형이 얼마나 설명력을 갖는가?
- 결정계수(R^2)를 확인한다. 결정계수는 0~1 값을 가지며, 높은 값을 가질수록 추정된 회귀식의 설명력이 높다.
3. 모형이 데이터를 잘 적합하고 있는가?
- 잔차를 그래프로 그리고 회귀진단을 한다.
회귀계수의 추정(최소제곱법)
측정값을 기초로 하여 적당한 제곱합을 만들고 그것을 최소로 하는 값을 구하여 측정결과를 처리하는 방법으로 잔차제곱이 가장 작은 선을 구하는 것을 의미한다.
2. 다중선형회귀분석(다변량회귀분석)
2개 이상의 동릭변수에 대하여 종속변수의 관꼐를 수치적으로 파악하기 위한 기법
실제 데이터와 오차가 가장 작아지는 회귀 방적식을 찾기 위해 최소제곱법을 활용
모형의 통계적 유의성
모형의 통계적 유의성은 F통계량으로 확인한다.
유의수준 5% 하에서 F통계량의 p-값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의하다고 본다.
| 요인 | 제곱합 | 자유도 | 제곱평균 | F-통계량 |
| 회귀 | 회귀제곱합(SSR) | k | MSR=SSR/k | F=MSR/MSE |
| 오차 | 오차제곱합(SSE) | n-k-1 | MSE=SSE/(n-k-1) | |
| 계 | 전체저곱합(SST) | n-1 |
F통계량이 크면 p-value가 0.05보다 작아지므로 귀무가설을 기각 할 수 있다.
오차(error)와 잔차(residual)의 차이
오차 : 모집단에서 실제값이 회귀선과 비교해볼 때 나타나는 차이(정확치와 관측치의 차이)
잔차 : 표본에서 나온 관측값이 회귀선과 비교해볼 때 나타나는 차이
회귀계수의 유의성
회귀계수의 유의성은 단변량 회귀분석의 회귀계수 유의성 검토와 같이 t통계량을 통해 확인한다.
모든 회귀계수의 유의성이 통계적으로 검증되어야 선택된 변수들의 조합으로 모형을 활용할 수 있다.
다중 공선성
다중회귀분석에서 설명변수들 사이에 선형관계가 존재하면 회귀계수의 정확한 추정이 곤란하다.
'통계 분석' 카테고리의 다른 글
| [Python] 정규성 검정 (0) | 2023.10.28 |
|---|---|
| [통계 분석] 모수 검정와 비모수 검정 (0) | 2023.10.27 |
| [기초 통계학] 회귀 분석 (1) | 2023.06.29 |
| [기초 통계학] 통계학 및 로마자 기호 모음 (0) | 2023.06.28 |
| [기초 통계학] 가설 검정(2) (0) | 2023.06.27 |

