가. 전수 조사, 표본 조사
전수 조사(총 조사 / 전수 조사) : 통계 분석을 수행하기 위해 조사 대상이 되는 모든 자료에 대해 데이터 수집을 실시하는것
ex) 대학민국 남성의 평균키를 조사하기 위해 대한민국의 모든 남성의 키를 조사하는것
표본 조사 : 통계 분석을 수행하기 위해 조사 대상이 되는 자료의 일부분에 대하여 데이터 수집을 실시하는것
ex) 대한민국 남성의 평균키를 조사하기 위해 모든 남서으이 키를 조사하는 것은 불가능에 가깝기 때문에 남성의 일부만 대상으로 해서 조사하는것
1. 용어 정리
- 모집단 : 조사하고자 하는 대상 집단 전체 ex) 대한민국 남성 정체
- 원소 : 모집단을 구성하느 개체
- 표본 : 조사하기 위해 추출한 모집단의 일부 원소
- 모수 : 표본 관측에 의해 구하고자 하는 모수에 대한 정보
나. 표본 추출 방법
- 표본은 조사 대상 정체를 잘 나타낼 수 있어야한다.
- 표본 추출 방법에 따라 결과가 달라질 수 있으므로 신중한 선택이 필요하다.
- 표본 추출은 활률 표본 추출과 비확률 표본추출로 나뉜다.
2. 확률 표본 추출
단순 랜덤 추출법(simple random sampling)
- N개의 모집단에서 n개의 표본을 추출하는 방법
- 샘플에 번호를 부여하여 임의의 n개를 추출하는 방법으로 각 샘플은 선택될 확률이 동일하다.
- ex) 제비 뽑기, 사다리타기
계통 추출법(systematic sampling)
- 단순 랜덤 추출번의 변형된 방식으로 번호를 부여한 샘플을 나열하여 K개 씩 n개의 구간으로 나누고 처 구간 에서 하나를 임의로 선택한 후 K개씩 띄어서 n개의 표본을 선택한다. 즉, 임의 위치에서 매 k번째 항목을 추출하는 방법이다.
- 간격을 얼마로 할지는 조사자의 선택이다.

집락 추출법(cluster random sampling)
- 모집단을 여래개의 군집으로 나눈후 군집별로 단순 랜덤 추출법을 수행하거나 추출된 군집을 전수조사 하는 방법
- 각각의 군집들은 서로 유사한 형태를 보유하고 있으므로 군집내 이질, 군집 간 동질이다.

층화 추출법(stratified random sampling)
- 집락 추출법과 유사한 추출법
- 군집화 할때 유사한 데이터를 하나의 군집으로 묶어서 층을 나눈 후 각 층에서 샘플을 추출 하는것으로 군집 내 동질, 군집 간 이질이다.
- 비례 층화 추출법과 불비례층화 추출 법으로 구분된다.
- 비례 층화 추출법 : 각 군집이 보유한 원소의 수에 비례하여 표본을 추출
불비례 층화 추출법 : 각 군집이 보유한 원소 수에 비례하지 않게 표본을 추출


다. 자료의 척도
| 질적 척도 (범주형 자료, 숫자들의 크기 차이가 계산 되지 않는 척도) |
명목 척도 | 측정 대상이 어느 집단에 속하는지 분류할 때 사용(성별, 대학교, 지역) |
| 순서 척도 | 측정 대상의 서열관계를 관측하는 척도(만족도, 선호도, 학년, 신용등급) | |
| 양적 척도 (수치형 자료, 숫자들의 크기 차이를 계산 할 수 있는 척도) |
구간 척도 (등간 척도) |
측정 대상이 갖고 있는 속성의 양을 측정하는 것으로 구간이나 구간 사이의 간격이 의미가 있는 자료(온도, 지수) 절대적 크기를 측정할 수없기 때문에 (+,-)는 가능하지만 (*,/)는 불가능하다. |
| 비율 척도 | 간격(차이)에 대한 비율이 의미를 가지는 자료, 절대적 기준인 0이 존재하고 사칙연산이 가능하며 제일 많은 정보를 가지는 척도(키, 몸무게,나이, 시간) 사칙연산이 모두 가능하다. |
라. 기초 통계량
- 평균(기댓값)
- 산술평균을 의미하며 데이터를 요약할때 가장 대표적으로 사용괴는 값이다.
- 단점) 이상값에 큰 영향을 받는다
- 중앙값
- 평균의 함정을 피하기 위한 하나의 척도, 자룔르 순서대로 나열했을때 가운데 위치한 값
- 최빈값
- 평균의 함정을 피하기 위한 하나의 척도로 자료 중 가장 발생 빈도가 높은 값
- 분산
- 자료들이 평균으로 부터 얼마나 멀리 떨어져 있는지 나타내는 척도
- 값이 클수록 자료들은 평균으로 부터 멀리 덜어져 있고, 분산이 작을 수록 평균에 가깝다.
- 단점) 분산의 단위는 기존 자료 단위의 제곱으로 통일된 형태가 아님
- 표준편차
- 분산의 단점을 보안하기 위해 등장한 척도
- 분산의 제곱근 값으로 분산과 동일하게 자료들이 평균으로 부터 얼마나 떨어져 있는지 나타내는 척도이다.
- 기존 자료들과 통일된 단위를 보유한다.
- 첨도
- 자료가 평균에 얼마나 많이 밀집해 있는지 나타내는 측도
- 첨도의 값이 3보다 작으면 멀리 흩어져 있고 3보다 크면 가운데 많이 밀집해 있으며, 첨도 값이 3인 경우 정규 분포의 형태를 나타낸다.

- 왜도
- 자료의 비대칭 정도를 나타내는 측도
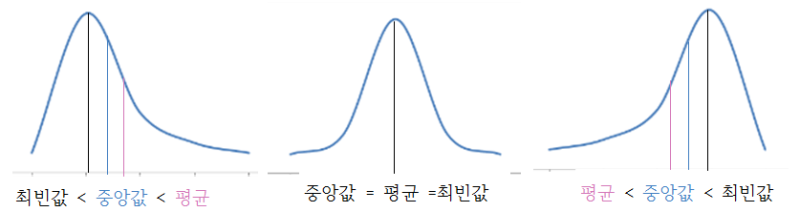
- 왜도가 음수이면 왼쪽으로 긴 꼬리를 가지는 형태이고 이때 평균이 가장 작고 다음이 중앙값 그리고 최빈값이 가장 큰 형태이다.(평균 < 중앙값 < 최빈값)
- 왜도가 양수이면 오른으로 긴 꼬리를 가지는 형태이고 이때 최빈값이 가장 작고 다음이 중앙값 그리고 평균이 가장 큰 형태이다.(최빈값 < 중앙값 < 평균)
- 왜도가 0인 경우 평균을 중심으로 완벽한 대칭구조를 가지는분포가 된다.
- 공분산
- 두 확률 변수 X,Y의 상관 정도를 나타내며 하나의 변수가 증가할 때 다른 변수의 증감여부를 알려준다.
- 0 < 공분산 : X가 증가할때 Y도 증가하는 형태
- 0 > 공분산 : X가 증가할때 Y는 감소하는 형태
- 0 = 공분산 : 증감에 관계없이 데이터가 규칙없이 뿌려진다.
- 단점) 최솟값, 최댓값이 존재하지 않아 상관정도를 확인 하기 힘들다.

- 상관계수
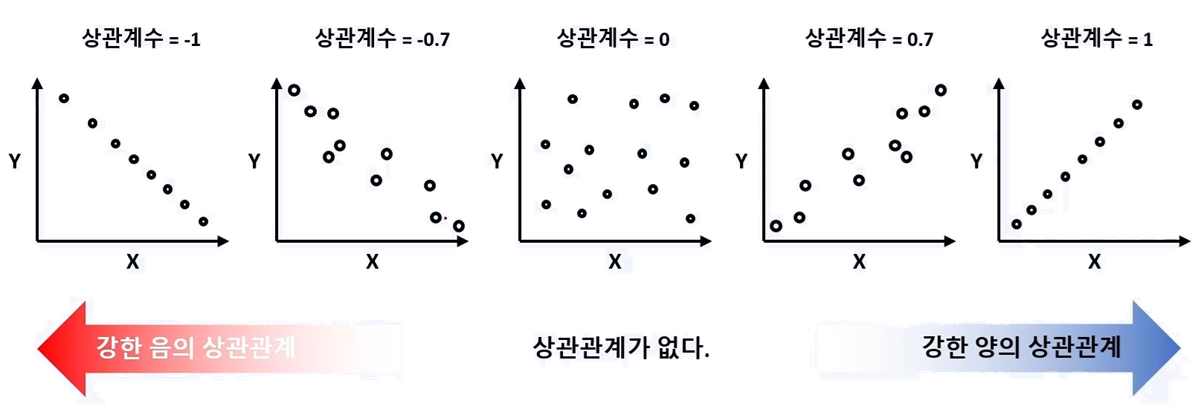
- 공분산의 단점을 보안하는 지표, -1 ~ 1사이의 값을 가진다
- 상관계수 -1에 가가울 수록 강한 음의 상관관계를 가지며, 1에 가까울 수록 강한 양의 상관관계를 가진다. 0에 가까워 질 수록 상관관계가 없음을 나타낸다.
* 척도와 측도의 차이
- 척도:
데이터 간의 관계를 설명하는 데 사용되는 분류체계
등간 척도, 비율 척도, 명목 척도, 순서 척도와 같이 여러 유형이 있다.
척도를 사용하면 데이터 간의 상대적 차이, 순서, 동일성 등을 파악할 수 있으나 절대적 기준을 가지지 않는다. - 측도:
변수의 실제 값을 나타내는 척도
데이터를 관찰 및 정량화하는데 사용된다.
산술 연산을 수행할 수 있으며, 절대적 기준을 가지고 있다.
요약 : 측도는 데이터의 실제 값을 나타내고 연산을 수행하는데 사용하는 반면, 척도는 데이터 간의 관계를 설명하기 위한 분류 체계다.
'통계 분석' 카테고리의 다른 글
| [기초 통계학] 회귀 분석 (1) | 2023.06.29 |
|---|---|
| [기초 통계학] 통계학 및 로마자 기호 모음 (0) | 2023.06.28 |
| [기초 통계학] 가설 검정(2) (0) | 2023.06.27 |
| [기초 통계학] 가설 검정 (0) | 2023.06.27 |
| [기초 통계학] 확률 분포 (0) | 2023.06.27 |

